为什么要学习线性代数

Published:

学习动机

空间想象给我们的直观感受

An image

线性代数提供一套便捷的概念和语言讨论空间，n维空间中的现象都可以从直观上进行理解，线性代数的本质就是对线性空间、向量和矩阵的直觉描述

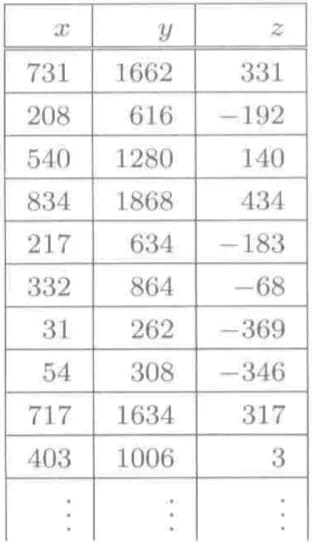
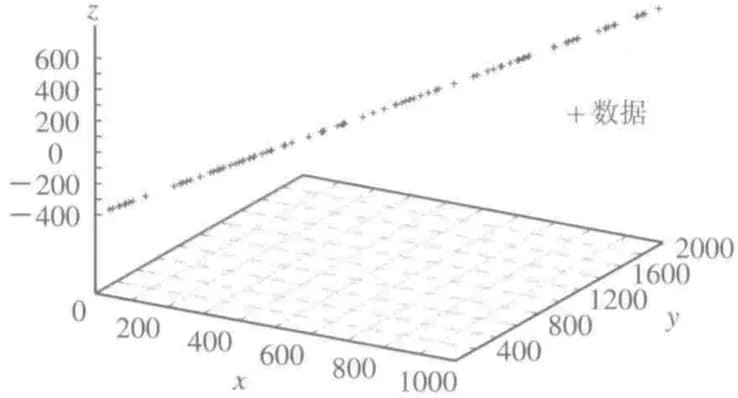
An image

An image

有效利用线性近似的手段

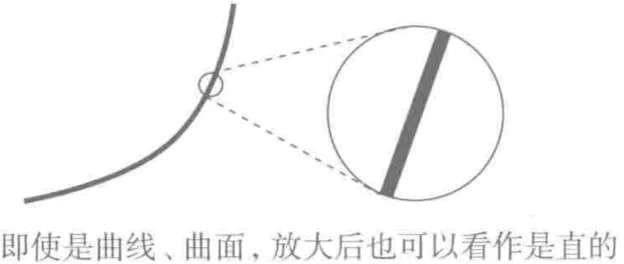
An image

An image

曲线在小范围进行分析，可以通过直线来进行近似

我对学习线性代数的理解：在人工智能、机器学习及其深度学习中，都需要一定量级的数据作支撑，线性代数是数据分析的关键工具，在这些领域通过线性代数来进行分析及其预测。

线性代数中的向量

向量与空间

—字面意思实际意思
向量排成一列(行)的数字有向线段、空间内的点
  1. 列向量
(13)(357)(23589)\begin{pmatrix} 1\\ 3\\ \end{pmatrix} \begin{pmatrix} 3\\ 5\\ 7\\ \end{pmatrix} \begin{pmatrix} 2\\ 3\\ 5\\ 8\\ 9\\ \end{pmatrix}
  1. 行向量
(a1,a2,⋯ ,an)(a_1,a_2,\cdots,a_n) (2,3,5,8)T=(2358)(2358)T=(2,3,5,8)(2,3,5,8)^T=\begin{pmatrix}2\\3\\5\\8\\\end{pmatrix}\quad {\begin{pmatrix}2\\3\\5\\8\\\end{pmatrix}}^T = (2,3,5,8)

为了书写方便，列向量通常写成转置写法

  1. 加法：相同维数的向量加法

    (x1⋮xn)+(y1⋮yn)=(x1+y1⋮xn+yn) \begin{pmatrix} x_1\\ \vdots\\ x_n\\ \end{pmatrix}+ \begin{pmatrix} y_1\\ \vdots\\ y_n\\ \end{pmatrix}= \begin{pmatrix} x_1+ y_1\\ \vdots\\ x_n+ y_n\\ \end{pmatrix}

  2. 数量乘法：任意常数c和向量的乘法

    c(x1⋮xn)=(cx1⋮cxn) c\begin{pmatrix} x_1\\ \vdots\\ x_n\\ \end{pmatrix}= \begin{pmatrix} cx_1\\ \vdots\\ cx_n\\ \end{pmatrix}

向量空间的形象

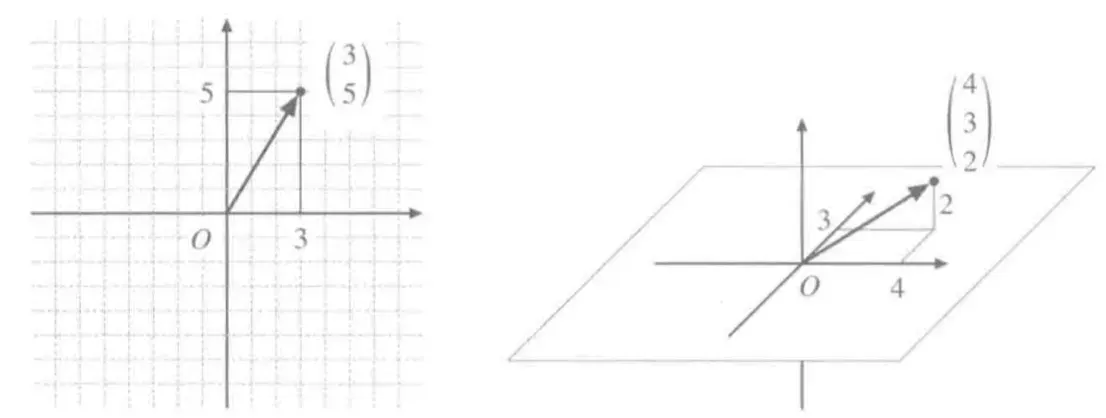
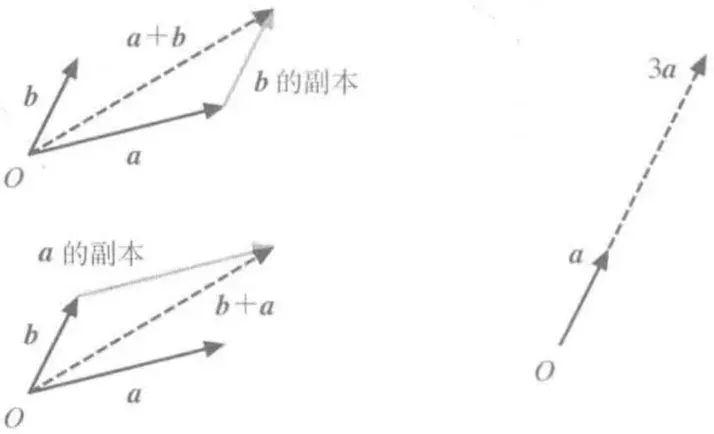
An image

An image

有向线段表示向量时，加法就是线段的连接，数量乘法就是线段的伸缩

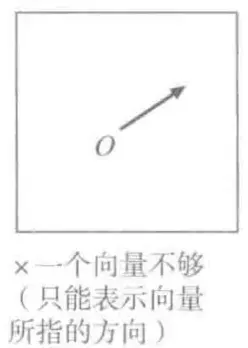
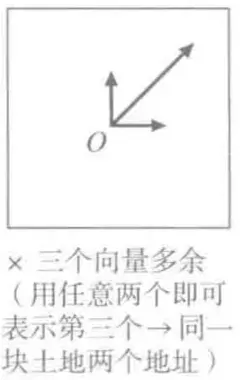
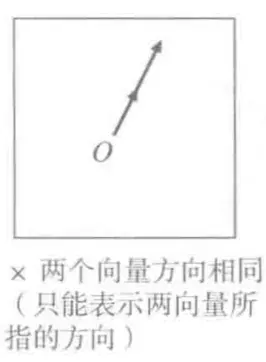
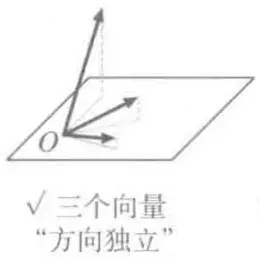
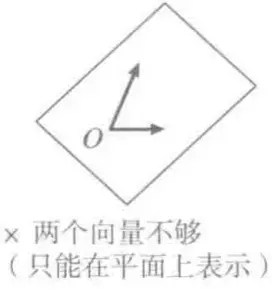
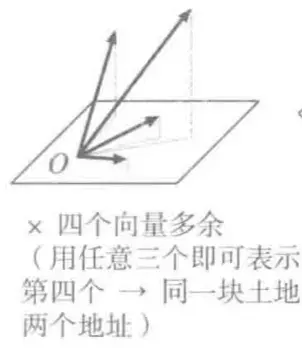
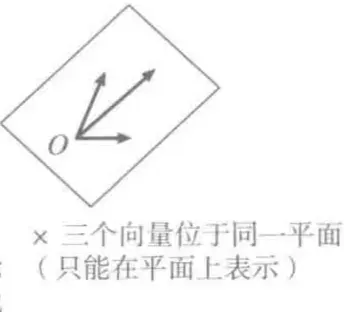
向量基底

没有刻度，没有特定方向，只有参照原点，依然可以进行加法和数量乘法，这个空间叫做向量空间（线性空间）

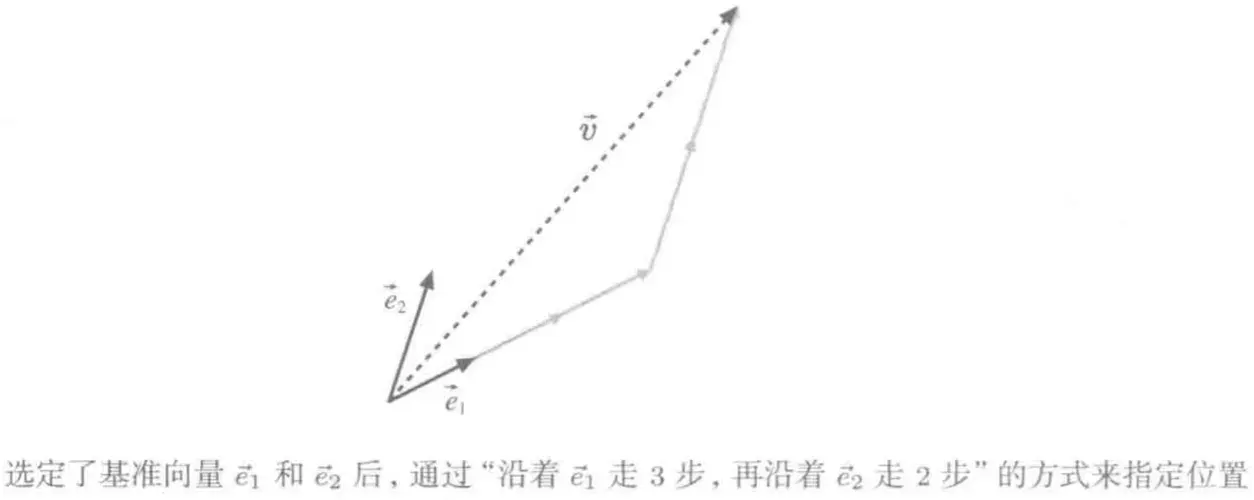
An image

  1. 作为基准的一组向量叫基底
  2. 沿着各个基准向量走的步数叫坐标
  3. e1、e2叫基向量
  1. 当前空间中任何向量都可以表示成： v⃗=x1e1⃗+⋯+xnen⃗\vec{v} = {x_1}\vec{e_1}+{\cdots}+{x_n}\vec{e_n}
  2. 这种表示方法是惟一的
a=[a1,a2,⋯ ,an]b=[b1,b2,⋯ ,bn]a= \begin{bmatrix}a_1,a_2,\cdots, a_n\end{bmatrix}\quad b= \begin{bmatrix}b_1,b_2,\cdots, b_n\end{bmatrix} ab=a1b1+a2b2+⋯+anbnab = a_1b_1+a_2b_2+ \cdots+ a_nb_n

An image

An image

An image

An image

An image

An image

An image

An image

矩阵和向量的关系

vector⊆matrixvector\subseteq matrix